personnumber3377
How I automated my geometry homework.
This is a story of how I automated my geometry homework (partly) (you can find the complete source code for this tool on: https://github.com/personnumber3377/Geometrylib ). (!!! NOTE: I MAY ADD UPDATES TO THIS BLOG LATER. THIS PROJECT IS NOT YET COMPLETELY FINISHED !!!)
The problem description:
Again after a long day at school I sat on my chair. Finally, some peace… Right? No. As, usual there is a pile of boring math homework to do. The problems are simple, but there are a crapton of them. Maybe I can automate this process somehow? I could use some tool like Geogebra, but I think that geogebra is a numerical tool, which only approximates the answers, so I think that I should use a tool which is both symbolic (instead of numeric) and which handles geometric objects well.
After a bit of googling I found out that such a tool does not exist, which is to my liking. Either they are too unintuitive, have poor programmability or are otherwise garbage. :( .
This is a slight writeup of me writing a geometry tool for myself.
Design choices:
I wanted this tool to be simple to use, but still give verbose output to the commands which you give it. Also I want it to handle unknown values for angles etc. , such that we can solve problems in the format: “Which point is x distance away from y and is on the circle z”-type questions. As an example: “Let there be three circles of radius one, which all are tangential to the two other ones. What is the radius of the circle which barely inscribe all of the three circles?”. The obvious way of doing this problem is to first find the center of the three circles and then get the length of the line from the center to the farthest point on any one of the circles. The length of that line is the answer to the problem. Reading this problem I am thinking of a command line and a command like “line a=a0 b=b0 c=c0” which creates a line of the format “a0x0+b0y+c0=0”. And then maybe I can implement a method such as get_constants_from_two_points(point1, point2) which updates those values in the line such that the line passes through those two points. Also I think that I can also implement a method such as Intersect which is similar to that of the intersect command in geogebra which returns the value(s) for x and y which satisfy the equations of both the objects, like intersect(object1, object2) .
Starting development
I started the development of this tool from the different kinds of objects I wanted to include in my program. I started with a line:
class line:
def __init__(self,a="unknown",b="unknown",c="unknown", name="line"):
#name_str = name+str(self.var_count)
# a*x+b*x=c
self.debug=False
count = 0
while str(name)+str(count) in get_names(global_objects):
count += 1
if count:
self.name = str(name)+str(count)
self.var_count = count
else:
self.name = name # there were no duplicates so just set the name as name
self.var_count = count
if name == "line":
print("self.var_count : " + str(self.var_count))
print("name: " + str(name))
name_str = name+str(self.var_count)
print("name_str : " + str(name_str))
self.name = name_str
else:
self.name = name
self.a = Symbol('a'+str(count))
self.b = Symbol('b'+str(count))
self.c = Symbol('c'+str(count))
self.x = Symbol('x'+str(count))
self.y = Symbol('y'+str(count))
if a != "unknown":
self.a = a
if b != "unknown":
self.b = b
if c != "unknown":
self.c = c
def set_values_point_line(point, line_vector):
# this basically gets the appropriate values for a,b,c when the line goes through point and steps from there to line_vector from point
# basically assume that c=1
#self.c_val = 1
self.c = 1
'''
xv = line_vector.item(0)
xy=line_vector.item(1)
x0 = point.item(0)
x1 = point.item(1)
'''
xv = line_vector[0]
xy=line_vector[1]
x0 = point[0]
x1 = point[1]
# a = -(yv/(x0*yv-xv*y0))
# b = xv/(x0*yv-xv*y0)
self.a = simplify(-(yv/(x0*yv-xv*y0)))
self.b = simplify(xv/(x0*yv-xv*y0))
#self.c = float(self.c)
#self.a = float(self.a)
#self.b = float(self.b)
return;
def set_values_two_points(point1, point2):
# get vector from point1 to point2
from1to2 = -1*point1+point2
self.set_values_point_line(point1, from1to2)
def get_equations(self):
# returns the line in the a*x+b*y+c = 0 format
equation = "("+str(self.a)+")*"+str(self.x)+"+("+str(self.b)+")*"+str(self.y)+"+("+str(self.c)+")"
right_side = "0"
if self.debug:
print(equation)
equation_left_side = parse_expr(equation)
print("oof")
equation_right_side = parse_expr(right_side)
print("oof22")
#return parse_expr(equation_left_side),parse_expr(equation_right_side)
return [Eq(equation_left_side, equation_right_side)]
def __str__(self):
return_string = '''=======================\nType: line\na = {}\nb = {}\nc = {}\nname = {}\n=======================
'''.format(self.a, self.b, self.c, self.name)
return return_string
That may seem overwhelming, but it actually isn’t that bad. I wanted to include this raw version of the line object, because when you look at some code online, you may feel like you are somehow inadequate as a programmer, but the fact that that said code has been combed over hundreds if not thousands of times to make it better has to be taken in to account. The first version of said code was most likely a messy piece of code, which just barely worked and was later polished finer. Also I forgot to mention that my code uses the sympy library to actually do the heavy lifting of solving the intersection points for example, so in that sense my code is just a wrapper around sympy, which just formats the user input from abstract concepts like lines and circles to mathematical equations, but I decided that this is still a useful blog to write for some people idunno.
The object implements the set_values_two_points method which i talked about earlier, which just takes two points as arguments and then updates the values of the line appropriately. The funny thing is that as of now (unix time 1677694441 ) my code actually doesn’t use this method yet.
Implementing the command line:
I wanted the command line to be as simplistic as possible, yet intuitive to use. I had the unix command line in mind where the command is first and then the (possibly optional) arguments are separated by spaces. Then what I have in mind is a python like syntax to run a method on an object. For example if i declare a line as simply “line name=exampleline”, then I want to be able to run something like “exampleline.set_values_two_points point_a point_b” to make the line go through two points.
Ok so after a bit of coding (now it is almost 2 am and the unix time now is 1677714427 (yeah, i live in gmt+2)), I have finally implemented a way to get an intersection of two lines. The funny thing is, that I haven’t even implemented points properly. 😅 Anyway. Before I do that I want to show you the code for the command line handler:
def command_mainloop(file=None):
print_banner()
line_counter = 0
lines = []
if file:
fh = open(file, "r")
lines = fh.readlines()
fh.close()
for i in range(len(lines)):
lines[i] = lines[i][:-1]
print("Running commands from file "+str(file)+".")
objects = []
commands = ["line", "intersect", "help", "quit", "objects"]
min_arg_lengths = [0,0,0,0,0]
max_arg_lengths = [3,2,0,0,0]
handle_functions = [line_command, intersection_command, help_command, quit_command, objects_command]
while True:
if line_counter != len(lines):
command_string = lines[line_counter]
line_counter += 1
print("Command string: " + str(command_string))
else:
command_string = str(input(bcolors.OKBLUE + ">>> " + bcolors.ENDC))
command_start = command_string.split(" ")[0]
if command_start not in commands:
if command_start != "":
if len(command_string.split(" ")) == 1:
# if the user types just the object name, then print object as string
if command_start in get_names(global_objects):
print_object(get_object_by_name(command_start))
continue
invalid_command(command_string)
continue
# first assume that the command is an attempt to run a method on an object:
result = check_method_command(command_string, global_objects)
if result: # 0 means success, 1 means failure
invalid_command(command_string)
continue
index = commands.index(command_start)
result = check_common_syntax(command_string, max_arg_lengths, min_arg_lengths, commands) # this check is shared by every command to check the arguments
if result:
continue
handle_functions[index](command_string, global_objects)
The “commands” is a list of all the commands as strings and “handle_functions” are the functions which handle the commands. A list of function pointers and then accessing the list by an index is probably asking for trouble, but I do not really give a shit. If the command is not in the commands list, then first assume that the command is either setting some attribute of an object or calling a method on an object. Now, I actually can not call the set_values_two_points method, because I haven’t implemented points properly, but that will soon change.
Now actually looking at my code, I realize that there are functions which need to be shared by all geometric objects, like run_method_on_self , which, as the name suggests, is used to run a method which the objects has, like the aforementioned set_values_two_points method for the line function. In fact, instead of implementing the point, I am first going to make the code less repetitive. I am going to first obviously make a copy of the working version, before I break something in the code.
After a bit of research, I actually realized that Sympy has also geometric methods to solve geometric problems, such as sympy.Line and sympy.Point . Oh well. It wasn’t all to waste, since I got some programming practice atleast. Also sympy doesn’t have some functionality, which I would like to have. For example it does not have a direct method to find the shortest path (or the longest path) between a circle and a line or another point. (By longest point I mean that the distance between the farthest point still on the circle and a point.).
Ok so after a bit of fiddling, I finally made a function which I can put to almost any object, and which automatically handles the arguments passed to the object. Now I do not need to copy paste that code in every object which I want to make. I also want this code to sort of be modular, such that people can add objects into it.
Oh, wait. After trying out the code, the code seems to actually not work. Back to debugging it is.
2nd of February 2023 :
Ok so now it is the next day (well actually I spent the morning sleeping and day doing something else. Now it is 5pm in the evening already.) .
After a bit of fiddling around, I found the bug. The bug is that because python uses pass by reference instead of pass by value. This is quite annoing in some cases where you want to make a copy of an object and then modify the copy of it instead of the original, as the case is in my code. This is what I am talking about:
(python3 shell)
>>> list1 = [1,2,3]
>>> list2 = list1
>>> list1.append(4)
>>> list2
[1, 2, 3, 4]
To make an actual copy of an object, instead of a copy of the pointer to the object, the “copy” library can be used. Like this:
>>> import copy
>>> list1 = [1,2,3]
>>> list2 = copy.copy(list1)
>>> list1.append(4)
>>> list2
[1, 2, 3]
And even this in some cases is inadequate, and in some cases the deepcopy method should be used instead of just copy.copy , but for my purposes this is adequate. Actually I do not even need to do any copying, because the bug occurs here in my code:
objects.append(new_object)
print("gregregregrr")
print("global_objects at the start: " + str(get_names(global_objects)))
print("objects after appending new_object: " + str(get_names(objects)))
global_objects.append(new_object) # <- bug occurs here
the “objects” object is a reference to “global_objects” and that is why when I append the object to first objects and then to global_objects , I am actually appending to the same list twice. The fix for this bug is to simply comment out the global_objects.append line like so:
objects.append(new_object)
print("gregregregrr")
print("global_objects at the start: " + str(get_names(global_objects)))
print("objects after appending new_object: " + str(get_names(objects)))
#global_objects.append(new_object) # <- no more bug :)
Now it is time to try to add this shared object creation code to the other objects, such as the circle and (yet to be implemented properly) points.
Now after a while I have implemented the shared init code for every one of the objects, but I still have to make this method a bit nicer and also more modular such that the same code can be used in every object:
def run_method_on_self(method_string, command):
# global_objects
args = command.split(" ")[1:]
if len(args) != self.num_args[self.num_args.index(method_string)]:
fail("Invalid number of arguments for method "+str(method_string)+" on object named "+str(self.name))
if method_string == "set_values_point_line":
obj1_name = args[0]
obj2_name = args[1]
point1 = get_object_by_name(obj1_name)
point2 = get_object_by_name(obj2_name)
if point1 == 1 or point2 == 1:
return 1
self.set_values_point_line(point1, point2) # the line vector is basically a point
return 0
if method_string == "set_values_two_points":
obj1_name = args[0]
obj2_name = args[1]
point1 = get_object_by_name(obj1_name)
point2 = get_object_by_name(obj2_name)
if point1 == 1 or point2 == 1:
return 1
self.set_values_two_points(point1, point2)
return 0
This is the current code for the line object and run_method_on_self as the name suggests runs a method which belongs to the object with certain arguments. This is will ultimately be used for things like “line.set_values_point_line yourpoint1 yourpoint2” which can not currently yet be done. That command then should set the appropriate values for a, b and c such that the line passes through those two points.
3rd of February 2023 (unix time 1677838933 around half past 12 am)
Ok so it is the new day again. Time to implement the points. Finally.
Currently the point object looks like this: (this is the very first version, before I decided to use sympy as my backend)
class point:
def __init__(self, x=None, y=None, vector=None):
if vector != None:
self.vector = vector
self.x=vector.item(0)
self.y=vector.item(1)
elif x==None and y==None:
warn("Warning. Uninitialized point.")
return
else:
self.vector = np.array([[x],[y]])
self.x = x
self.y = y
def set_property_on_self(self,selected_property, value):
# thanks to https://stackoverflow.com/questions/2612610/how-to-access-get-or-set-object-attribute-given-string-corresponding-to-name-o
# stackoverflow username @pratik-deoghare
# setattr(t, 'attr1', 21)
print("selected_property: "+str(selected_property))
print("value: "+str(value))
setattr(self, selected_property, value)
return 0
The set_property_on_self is copied from the others, because it should a method of every geometric object. (Maybe I can achieve this with inheritance instead of copy pasting it everywhere?), but the init function is lacking.
Oh, by the way, the init function of the line for example now has been replaced by this:
def __init__(self,*arguments):
#name_str = name+str(self.var_count)
# a*x+b*x=c
self.debug=False
self.default_arguments = {"a":"unknown", "b":"unknown", "c":"unknown", "name":"line"}
self.methods = [self.set_values_point_line, self.set_values_two_points, self.get_equations, self.noop]
self.method_strings = ["set_values_point_line", "set_values_two_points", "get_equations", "noop"] # the noop is just for sanity testing
self.method_arg_types = [["point", "point"], ["point", "point"], [], []]
self.num_args = [2,2,0,0] # these are strict number of arguments for each method
self.parameters = ["a","b","c","x","y"]
common_arg_stuff(self, *arguments)
The common_arg_stuff is the function which handles the arguments regardless of which object it is (circle, line etc), such that I can use the same template for everything instead of copy pasting stuff, for example the new init function for the circle is this:
def __init__(self, *arguments):
self.debug=False
self.default_arguments = {"xc":"unknown", "yc":"unknown", "r":"unknown", "name":"circle"}
self.methods = [self.replace_equation_shit, self.get_equations]
self.method_strings = ["replace_equation_shit", "get_equations"]
self.num_args = [0,0]
self.parameters = ["xc", "yc", "r", "x", "y"]
common_arg_stuff(self, *arguments)
Looks pretty much the same, right? Pretty neat.
Anyway, back to the point(s). :)
Now after a bit of coding, here is the finished point class:
class point:
def __init__(self, *arguments):
self.debug = False
self.default_arguments = {"x":"unknown", "y":"unknown", "name":"point"}
self.methods = [self.set_point_to_values, self.get_equations]
self.method_strings = ["set_point_to_values", "get_equations"]
self.method_arg_types = [["float", "float"], []]
self.num_args = [2, 0]
self.parameters = ["x", "y"]
common_arg_stuff(self, *arguments)
def set_point_to_values(self, x, y):
self.x = x
self.y = y
return 0
def set_property_on_self(self,selected_property, value):
# thanks to https://stackoverflow.com/questions/2612610/how-to-access-get-or-set-object-attribute-given-string-corresponding-to-name-o
# stackoverflow username @pratik-deoghare
# setattr(t, 'attr1', 21)
print("selected_property: "+str(selected_property))
print("value: "+str(value))
setattr(self, selected_property, value)
return 0
def get_equations(self):
left_side_1 = "x"
left_side_2 = "y"
right_side_1 = str(self.x)
right_side_2 = str(self.y)
equation_list = [Eq(left_side_1, right_side_1), Eq(left_side_2, right_side_2)]
return equation_list
def __str__(self):
return '''=======================\nType: point\nx = {}\ny = {}\nname = {}\n=======================\n'''.format(self.x, self.y, self.name)
The set_point_to_values method is used to do a thing like mypoint.set_point_to_values x=1 y=2 to set the point to anything we want.
Then to check if a point is on some geometric object we can do intersect point object . Actually, I am going to test if that works now.
Actually I forgot the run_method_on_self method for the point, so I am adding it now to it. I should really propably try to do the inheritance thing.
…
There. Now this works: “point0.set_point_to_values 1 2” and then “point0” returns this:
=======================
Type: point
x = 1.0
y = 2.0
name = point0
=======================
Now it is almost 2 am again and unix time 1677886826 and I have finally a somewhat functional program. Now you can solve the intersection between circles, lines and points. I had to tweak the intersection command, becasue the way Sympy handles variables and variable names was a bit wack.
def intersection(object1, object2):
# object is assumed to have the get_equation method which returns the equation which describes the object (like a line is a*x+b*y+c=0 )
print("================================================")
print("object1 : " + str(object1))
print("object2 : " + str(object2))
print("object1 : " + str(type(object1)))
print("object2 : " + str(type(object2)))
print("================================================")
equations1 = object1.get_equations()
equations2 = object2.get_equations()
results = []
temp_var_x = Symbol("tempvarx")
temp_var_y = Symbol("tempvary")
substituted_equations = []
for equation in equations1:
substitute_first = {"x":temp_var_x, "y":temp_var_y}
#substitute_second = {"x"+str(object1.var_count):temp_var_x, "y"+str(object1.var_count):temp_var_y}
equation1 = equation.subs(substitute_first)
substituted_equations.append(equation1)
for equation in equations2:
substitute_first = {"x":temp_var_x, "y":temp_var_y}
#substitute_second = {"x"+str(object1.var_count):temp_var_x, "y"+str(object1.var_count):temp_var_y}
equation1 = equation.subs(substitute_first)
substituted_equations.append(equation1)
result = sympy.solve(substituted_equations, (temp_var_x, temp_var_y))
print("result: "+str(result))
return result
So it basically works by setting the x and y in each of the equations to one variable. Now thinking about it can I just solve the equations in one go without an intermediate variable??
…..
Yeah, I am a bit dim it seems. This works 100% fine, so all of that tweaking of the last hour went to waste :)
This works all right too:
def intersection(object1, object2):
equations1 = object1.get_equations()
equations2 = object2.get_equations()
all_equations = equations1 + equations2
result = sympy.solve(all_equations, ('x', 'y'))
print("result: "+str(result))
return result
I should really stop overthinking stuff.
Adding even more features
Next I want to implement the distance thing. Actually, I want to implement a distmin and a distmax function, which as the name suggests gets the minimum distance and the maximum distance between two objects.
For example the maximum distance between a circle and a point is the distance from the point to the point on the circle which is on the opposite side of the circle from the point. So the distmax function is defined as the maximum distance of any two points, such that those points still lie on the objects. I think that this is a bit too hard to implement, so I will first implement it for a point and an object, ill call it mindistobjdot and maxdistobjdot
After doing a bit of googling I stumbled upon this: https://computationalmindset.com/en/mathematics/experiments-with-sympy-to-solve-odes-1st-order.html which tells how to solve a differential equation in python sympy.
The way I want to go about this is to get the equation for the object and then make a function for the distance between the point and the object and then find the minimum of that using the derivative of it.
First let us make a function to make an expression for the distance:
I am actually going to go to sleep now. See ya in the morning.
Ok now it is unix time 1678043310 .
When modifying the intersection command I actually did something which makes it not work for lines. … After a bit of debugging I found that I haven’t updated the get_equations method for a line appropriately, because it was returning : ax0 + by0 + c = 0 instead of ax+by+c=0 .
Ok so after again a bit of debugging i have finally made a function which gets the minimum distance between a dot and another object. Except that there is a problem that it checks it by solving the differential equation by setting it to zero. Where a derivative is zero can also be the maximum distance. .. After a bit of digging I found this https://stackoverflow.com/questions/39192643/finding-the-minimum-of-a-function-on-a-closed-interval-with-python and once again, it seems that there is already a function which gets the minimum and maximum value of a function in a specified interval.
Currently my code looks like this:
def distance_min(object, point):
x1 = point.x
y1 = point.y
x0 = 'x'
object_equation = object.get_equations()[0] # support only a thing which has a single equation per object for now :)
print("object_equation : "+str(object_equation))
y0 = sympy.solve(object_equation, 'y') # make it of the form: y=...
y0 = y0[0]
print("y0 : "+str(y0))
x = sympy.Symbol('x')
distance_function = distance_thing(x0,y0,x1,y1) # at this point in a case where there are all known values for the objects this should return a function which only has one variable: "x"
print("distance_function : "+str(distance_function))
# thanks to https://computationalmindset.com/en/mathematics/experiments-with-sympy-to-solve-odes-1st-order.html
f = symbols('f', cls=Function) # make the distance function
f = distance_function
# now solve the differential equation to get min distance
#diff_eq = Eq(f(x).diff(x), 0) # f'(x) = 0
#oof = sympy.Derivative(distance_function, 'x')
#print("oooff : "+str(oof))
#diff_eq = Eq(distance_function, 0)
derivative = distance_function.diff('x')
equation = Eq(derivative, 0)
solution = solve(equation) # solve the equation
solution.append(y0.subs({'x':solution[0]}))
return solution
Actually the sympy.minimum function gives the minimum value, not the value of x for the function which gives the minimum value. We can fix this problem by getting the intersection between a circle of that radius and the point as the center.
We can easily implement maxdistobjdot by replacing minimum with maximum.
7th of March 2023. Ok so now it is actually 3am as I am writing this. I have exams coming up so I do not have that much time to program or do anything else, but I think I can manage it.
Now while implementing the min distance function, I came across a bug (once again).
def get_circle_eq(xc,yc,r):
print("Returning this: "+str("(x-{})**2+(y-{})**2=({})**2".format(xc,yc,r)))
return [Eq(parse_expr("(x-{})**2+(y-{})**2".format(xc,yc)), parse_expr("({})**2".format(r)))]
this code was originally this:
def get_circle_eq(xc,yc,r):
print("Returning this: "+str("(x-{})**2+(y-{})**2=({})**2".format(xc,yc,r)))
return [Eq(parse_expr("(x-{})**2+(y-{})**2".format(xc,yc)), parse_expr("{}**2".format(r)))]
See the difference? There are braces in the top one which aren’t in the bottom one. This caused the expression to be evaluated improperly leading to a wrong answer. Anyway, here is the complete code for the mindistobjdot:
def mindistobjdot(command:str, objects:list):
# the first object can be anything, but the second argument must be a point
arguments = command.split(" ")
arguments = arguments[1:]
object_thing = get_object_by_name(arguments[0])
dot_thing = get_object_by_name(arguments[1])
solution = distance_min(object_thing, dot_thing, maximumthing=False)
if solution == []:
print("No results for some reason")
return 0
else:
print("Minimum distance: " + str(solution))
return solution
return 0
and distance_min:
def distance_min(object, point, maximumthing=False):
x1 = point.x
y1 = point.y
x0 = 'x'
object_equation = object.get_equations()[0] # support only a thing which has a single equation per object for now :)
print("object_equation : "+str(object_equation))
y0 = sympy.solve(object_equation, 'y') # make it of the form: y=...
y0 = y0[0]
print("y0 : "+str(y0))
x = sympy.Symbol('x')
distance_function = distance_thing(x0,y0,x1,y1) # at this point in a case where there are all known values for the objects this should return a function which only has one variable: "x"
print("distance_function : "+str(distance_function))
# thanks to https://computationalmindset.com/en/mathematics/experiments-with-sympy-to-solve-odes-1st-order.html
f = symbols('f', cls=Function) # make the distance function
f = distance_function
if not maximumthing:
solution = minimum(distance_function, x)
else:
solution = maximum(distance_function, x)
print("solution: "+str(solution))
print("distance_function : "+str(distance_function))
return solution
It uses the minimum and maximum functions, which basically internally do what I originally did, aka solve the equation f’(x)=0 and then output the value of the original function at that point, except that in addition to my original version of the program, it also checks that the answer is actually the minimum value, and not for example the maximum value. If the derivative is zero, then that means that it can also be the maximum or a saddle point in addition to the minimum value. I probably should have implemented that myself as an exercise but whatever.
Note that this function returns the minimum or maximum distance, not the point which gives said distance. After a bit of digging I found out that the minimum function actually internally does something like this: (copied from the sympy source code)
if isinstance(symbol, Symbol):
if domain is S.EmptySet:
raise ValueError("Minimum value not defined for empty domain.")
return function_range(f, symbol, domain).inf
else:
raise ValueError("%s is not a valid symbol." % symbol)
and function_range is this (only part of it):
for is_open, limit_point, direction in bounds:
if is_open:
critical_values += FiniteSet(limit(f, symbol, limit_point, direction))
vals += critical_values
else:
vals += FiniteSet(f.subs(symbol, limit_point))
solution = solveset(f.diff(symbol), symbol, interval)
if not iterable(solution):
raise NotImplementedError(
'Unable to find critical points for {}'.format(f))
if isinstance(solution, ImageSet):
raise NotImplementedError(
'Infinite number of critical points for {}'.format(f))
critical_points += solution
for critical_point in critical_points:
vals += FiniteSet(f.subs(symbol, critical_point))
left_open, right_open = False, False
if critical_values is not S.EmptySet:
if critical_values.inf == vals.inf:
left_open = True
if critical_values.sup == vals.sup:
right_open = True
range_int += Interval(vals.inf, vals.sup, left_open, right_open)
so I was actually right that it basically solves the equation f’(x)=0 , but it also has some extra checks to check that the answer which it gives is actually the minimum/maximum. This is done by finding the critical points in the interval. The critical points are basically just the solutions to that differential equation. the range_int is a range of all possible values which the function can get. The minimum value is therefore the lower bound of this range and the maximum value is the higher bound of this. the range_int in addition to the solutions to the differential eq also has these:
for interval in interval_iter:
if isinstance(interval, FiniteSet):
for singleton in interval:
if singleton in domain:
range_int += FiniteSet(f.subs(symbol, singleton))
and
intervals = continuous_domain(f, symbol, domain)
range_int = S.EmptySet
if isinstance(intervals,(Interval, FiniteSet)):
interval_iter = (intervals,)
elif isinstance(intervals, Union):
interval_iter = intervals.args
so the range_int is initialized to have the values of the function at the bounds of its domain aka the bounds where the function is defined. For example the maximum distance between a point and a line is obviously infinity, and the distance function is defined for every real x, so the interval_iter gets appended by -oo and +oo where oo means infinity. So this is all to just to say. that the maximum/minimum of a function is at either at the edge of its domain (the smallest or the largest value of x for which the function is defined) or at a point where its derivative equals zero. I hope I explained this clearly. Feel free to ask for clarification.
To actually get the point which is the maximum or minimum distance away from the other point, we can just use the formula for a circle and set the radius as the distance. This is where the get_circle_eq function comes in:
def mindistpointobjdot(command:str, objects:list):
arguments = command.split(" ")
arguments = arguments[1:]
radiuses = mindistobjdot(command, objects)
point = get_object_by_name(arguments[1])
other_object = get_object_by_name(arguments[0])
equations = other_object.get_equations()
print("radiuses : "+str(radiuses))
radius = radiuses
x = sympy.Symbol('x')
y = sympy.Symbol('y')
'''
all_equations = equations1 + equations2
print("All equations as a list: "+str(all_equations))
result = sympy.solve(all_equations, ('x', 'y'))
print("result: "+str(result))
'''
circle_equation = get_circle_eq(point.x, point.y, radius)
print("circle_equation : "+str(circle_equation))
equations += circle_equation
print("all equations: "+str(equations))
result = sympy.solve(equations, ('x', 'y'))
print("Result: "+str(result))
So this is another command to actually get the point which we want. It internally uses the mindistobjdot command to get the min distance and then just checks the intersection between a circle of that radius centered at the other dot and the other object. We can simply implement this also for the maximum, by replacing mindistobjdot by maxdistobjdot. Now we can finally run something like:
line a=1 b=2 c=3
line0.name = myline
point
point0.name = mypoint
mypoint.set_point_to_values 0 0
mindistpointobjdot myline mypoint
quit
and this returns:
Result: [(-3/5, -6/5)]
which is correct!
Solving the original problem
Ok so to get the radius of the big circle which encompassesall the other circles, we need to get the maximum distance from the center of the three circles to any one of the other circles. First get the center of the third circle using two circles with radius 2 (one is at 0 0 and the other one is at 2 0). :
circle
circle0.name = mycircle1
mycircle1.xc = 0
mycircle1.yc = 0
mycircle1.r = 2
circle
circle0.name = mycircle2
mycircle2.xc = 2
mycircle2.yc = 0
mycircle2.r = 2
intersect mycircle1 mycircle2
returns:
Objects intersect atleast at one point.
Intersections are at points: [(1, -sqrt(3)), (1, sqrt(3))]
Then we can calculate the center of the three circle middles which is just the sum of the x coordinates/3 and the sum of the y coordinates/3 (i should really program a feature which calulates this). After that just find the max distance of that point and one of the circles and that is the answer:
circle
circle0.name = mycircle1
mycircle1.xc = 0
mycircle1.yc = 0
mycircle1.r = 1
point x=((1+2+0)/3) y=(sqrt(3)/3)
point0.name = mypoint
maxdistobjdot mycircle1 mypoint
quit
And the result is……:
Maximum distance: sqrt(12*sqrt(3) + 21)/3
which is roughly 2.15 , which is the right answer!
Is it actually useful?
Now pondering about it afterwards I am actually sceptical of the use cases of this tool. There are still a lot of features which comes to mind to me, for example more methods for lines, for example make a line which goes through a point and which points a certain way. This is of course just simple geometry to figure out the vector from the given angle between 0 and 360 degrees, but still. Also my tool lacks variable assignment and also I think that it would be handy to be able to define user defined functions more easily than implementing them by yourself into the code of the tool itself. Maybe something like myfunction(arg1,arg2,arg3):= maxdistobjdot (arg3) intersect(arg1, arg2)[0] as like a way to define a shorthand for the max distance of an object and an intersection. Also accessing the results of an operation by index for example to make a dot out of an intersection you could do something like point (intersect obj1 obj2)[0] and it could like automatically parse the arguments.
Now, I am not convinced that this tool is useful, so lets actually try it on another problem, which I haven’t looked at before:
Now here is a very interesting problem: Let the sides of a triangle be of lengths 356, 558 and 762 . The triangle is divided along the middle of the biggest angle. How many percent is the smaller one of the bigger one? This problem can be solved by using the law of sines: sin(a)/x=sin(b)/y=sin(c)/z where a b c are the angles of the opposite side of the sides x, y and z. Our tool now does not have the law of sines in it, but you can just use the sympy solver to solve the equation directly. However, technically you can use my tool to solve the problem, because you can figure out the points by using the circle and the intersection tool, then you can halve the angle by just taking a point which is halway through one of the sides of the triangle. Then you can just use the mindistobjdot to get the height of the triangle and you can calculate the area of the tiny triangle and then you can subtract that from the original triangle to get the area of the bigger triangle and then you are basically done. To do this using a script file as input to solve this problem, I need to implement the passing arguments by index and also assign variables to any value in the shell, because then I do not have to manually set the return values of an operation to operands to another command. Anyway, maybe I will do that soon. (To be continued…..)
Now it is unix time 1678233587 and now I am going to try to actually calculate that problem using my tool:
First we want to figure out the points of the triangle. I am going to pick the 356 length side to be the distance between (0,0) and (356,0) . Then I am going to set a circle of radius 762 at (0,0) and a circle of radius 558 at (356, 0). Then we want to get the intersection of those two and that is our third point of the triangle:
circle xc=0 yc=0 r=762
circle0.name = origincircle
circle xc=356 yc=0 r=558
circle0.name = anothercircle
intersect anothercircle origincircle
quit
Intersections are at points: [(49502/89, -4*sqrt(134302070)/89), (49502/89, 4*sqrt(134302070)/89)]
There is our third point. Now we need to figure out the largest angle:
sin(x)/356=sin(y)/558
sin(y)/558=sin(z)/762
and
x+y+z=180 degrees
Now if we solve these equations by just using a normal calculator:
[sin(x)/356=sin(y)/558, sin(y)/558=sin(z)/762, x+y+z=180]
we get:
[[25.854419252,43.1199594033,111.025621345]]
as x,y,z . Therefore angle z aka the angle which is opposite from the line which goes from the origin to the intersection point which we calculated. When the angle is halved, the intersection point is therefore halway of the intersecting line, therefore the point for the new triangle is (49502/89, 4*sqrt(134302070)/89)/2 because it is halway through the line. Now, there is a formula for the area of a triangle given its corners and it is:
A = 1/2(x1(y2-y3)+x2(y3-y1)+x3(y1-y2))
so we just plug in the numbers:
and we get a widly wrong answer. I was actually mistaken, going halfway through the line does not necessarily give you half the angle. We need to solve this using the angle. We know that the line passes through the point (356,0) and it impacts the x-axis in roughly 55.5 degrees. The derivative of the line is tan(55.5) . Lets solve it using a normal calculator:
[m*356+b=0,m=tan(55.5)]
[[1.45500902867,-517.983214207]]
so the line is 1.455009x-517=y aka 1.455x-y-517=0 aka a=1.455 b=-1 and c=517 . Now we need to find the intersection point between this and the side of the triangle which we can actually use our tool for with the set_values_two_points method.
line a=1.455 b=-1 c=-517.0
line0.name = halwayline
line
line0.name = side
point x=0 y=0
point x=49502/89 y=4*sqrt(134302070)/89
side.set_values_two_points point0 point1
intersect side halwayline
quit
Intersections are at points: {x: 216.190149213582, y: 202.443332894238}
Now we can use the triangle area formula:
area of smaller triangle:
a(0,0,216, 202,356,0) = -35956.0 (the are is obviously the absolute value of that)
the area of the bigger triangle is:
a(0,0,49502/89, 4*sqrt(134302070)/89,356,0) -92711.0159582
-35956/(-92711.0159582+35956) 0.6335299073209942
so roughly 64 percent. Aannd it is the right answer.
Variable assignment and getting output of a command to a list.
So one thing which I would like to add is a way to pass a result of another command as an argument to a creation of an object without having to manually type the values.
I would really like to do something like
point name=mypoint
point x=3 y=4 name=anotherpoint
set mypoint anotherpoint
To copy the values from anotherpoint to mypoint
and also I would like to do something like:
line a=1 b=2 c=3 name=myline1
line a=4 b=5 c=6 name=myline2
resultlist := intersect myline myline2
point [resultlist] name=mypoint
To pass the values of resultlist as like a list and then the parser could expand it for us. Now I am thinking that the initial command parser looks up a list called declared_variables, which has a list of objects, which has a list of variables a user has defined. Variables are basically a list of values which are the result of an operation.
Time to start coding…
After a bit of coding I came up with this:
def unpack_variables_in_command(command_string:str, user_defined_variables: list):
tokens = command_string.split(" ")
generated_command = []
for token in tokens:
if "[" not in token or "]" not in token: # if there is nothing to unpack then just append as is
generated_command.append(token)
else:
if token.count("[") > 1 or token.count("]") > 1:
fail("Subtokens like [myvar][a:b] are not implemented.")
return 1
var_name = token[token.index("[")+1:token.index("]")] # get the variable name from inside the brackets
if var_name not in user_defined_variables.keys():
fail("Undefined variable: "+str(var_name)+" .")
return 1
var_values = user_defined_variables[var_name]
print("str(var_values) == "+str(str(var_values)))
replacement = ' '.join([str(key)+str("=")+str(var_values[key]) for key in var_values.keys()])
generated_command.append(replacement)
final_command = ' '.join(generated_command)
return final_command
and this:
def variable_assignment_command(command_string: str, global_objects: list, max_arg_lengths: list, min_arg_lengths: list, commands: list) -> int:
tokens = command_string.split(" ")
if tokens[1] != ":=":
fail("Invalid variable assignment command: "+str(command_string))
return 1
# the new variable name is tokens[0]
new_var_name = tokens[0]
assigning_command = tokens[2:] # the command is after the "variable :=" part .
new_command_string = ' '.join(assigning_command)
result = check_common_syntax_var(new_command_string, max_arg_lengths, min_arg_lengths, commands) # this check is shared by every command to check the arguments
if result:
return 1
commands = ["line", "intersect", "help", "quit", "objects", "circle", "point", "mindistobjdot", "maxdistobjdot", "mindistpointobjdot", "maxdistpointobjdot"]
index = commands.index(new_command_string.split(" ")[0])
handle_functions = [line_command, intersection_command, help_command, quit_command, objects_command, circle_command, point_command, mindistobjdot, maxdistobjdot, mindistpointobjdot, maxdistpointobjdot]
var_values = handle_functions[index](new_command_string, global_objects)
print("var_values : "+str(var_values))
user_defined_variables[new_var_name] = var_values
print("var_values.keys()" + str(var_values.keys()))
print(str([str(a) for a in var_values.keys()]))
print(str([str(a) for a in var_values.values()]))
return 0
it basically runs the command after the “:=” part and then stores the result of that into the user_defined_variables list as a result. The user_defined_variables is just a global dictionary
now we can run:
line a=1 b=2 c=3
line0.name = myline1
line a=4 b=5 c=6
line0.name = myline2
myvar := intersect myline1 myline2
point [myvar]
point0.name = mypoint
mypoint
quit
and the result will be:
=======================
Type: point
x = 1
y = -2
name = mypoint
=======================
, so it works. This assumes that the function actually returns the results of the operation. Now, I haven’t yet implemented accessing the subscripts of these variables, for example you can not access myvar[0] yet, but I will probably implement that some time. Actually, I am going to implement it now.
Ok so after a bit of tinkering I modified the unpack_variables_in_command function and added this to it:
if token.count("[") > 1 or token.count("]") > 1:
# get only partial part of the result:
partial = token[token.index("]")+1:] # get the rest of the thing
start = partial[1:partial.index(":")]
end = partial[partial.index(":")+1:partial.index("]")]
start = int(start)
end= int(end)
#fail("Subtokens like [myvar][a:b] are not implemented.")
#return 1
var_name = token[token.index("[")+1:token.index("]")] # get the variable name from inside the brackets
if var_name not in user_defined_variables.keys():
fail("Undefined variable: "+str(var_name)+" .")
return 1
var_values = user_defined_variables[var_name]
print("str(var_values) == "+str(str(var_values)))
print("start == "+str(start))
print("end == "+str(end))
if start != None and end != None:
print("abcdefg")
# print({k:d[k] for k in l if k in d})
'''
d = {1:2, 3:4, 5:6, 7:8}
# the subset of keys I'm interested in
l = (1,5)
'''
l = tuple([list(var_values.keys())[x] for x in range(start, end)])
print("l == "+str(l))
var_values = {k:var_values[k] for k in l if k in var_values}
Now, another feature which I would like to add is to get the area between two graphs from their other intersection point to the other.
![area_example][/pictures/area_example.png]
The purple graph is basically the line-circle at that point and to get the area between those two graphs is just the area of the circle between the intersection points. Now I have an idea of how I would go about doing this, but it is a bit complex. I am thinking of first getting the equations and then converting them to the form y=blablabla and then taking the absolute value of their difference and then integrating that function over that range given by the intersection points. I think that it would be easiest to first just implement an “integral” command which is just a wrapper around the integral function of Sympy. I think that I am going to do that first:
def integrate_command(command: str, objects: list):
# integrate a function over xstart to xend
tokens = command.split(" ")
selected_object = tokens[1]
int_var = tokens[2] # variable is assumed to be next
xstart = tokens[3]
xend = tokens[4]
expression = None
if selected_object not in get_names(global_objects):
# the input is assumed to be a literal expression
equation = Eq(parse_expr(selected_object[:selected_object.index("=")]), parse_expr(selected_object[selected_object.index("=")+1:]))
expressions = [equation]
else:
expressions = get_object_by_name(selected_object).get_equations()
# if there are multiple equations for the object, then make the user choose which of them:
if len(expressions) > 1:
warn("The object you selected has multiple equations associated with it: ")
count = 0
for expr in expressions:
print(CBLUE +str("[{}] ".format(count)) + str(expr)+bcolors.ENDC)
count += 1
print("Please select the index of the desired expr: ")
index = int(input("> "))
selected_expr = expressions[index]
else:
selected_expr = expressions[0]
x = Symbol('x')
y = Symbol('y')
print("selected_expr: "+str(selected_expr))
y_function = solve(selected_expr,y)
print("y_function: " +str(y_function))
y_function = y_function[0]
result = integrate(y_function,(x,xstart, xend))
print(CYELLOW + "Result: "+str(result) + bcolors.ENDC)
return result
This seems adequate for now. Next I want to do the intersection thing:
def area_between_intersections(command:str, objects:list):
# calculate the area between the two intersection points of two graphs
# the syntax for this problem would be "commandstring" object1 object2
# parse command
tokens = command.split(" ")
equation_list = []
# get equations from the arguments: (I should probably makes this a function in itself to check if an arguments a raw expression or an object itself. )
for i in range(1,3):
object_name = tokens[i]
if object_name not in get_names(objects):
# assumed to be a raw expression
equation = Eq(parse_expr(object_name[:object_name.index("=")]), parse_expr(object_name[object_name.index("=")+1:]))
expressions = [equation]
else:
# object
expressions = get_object_by_name(selected_object).get_equations()
if len(expressions) > 1:
warn("The object you selected has multiple equations associated with it: ")
count = 0
for expr in expressions:
print(CBLUE +str("[{}] ".format(count)) + str(expr)+bcolors.ENDC)
count += 1
print("Please select the index of the desired expr: ")
index = int(input("> "))
selected_expr = expressions[index]
else:
selected_expr = expressions[0]
equation_list.append(selected_expr)
# get intersection points:
# def intersection(object1, object2):
'''
all_equations = equations1 + equations2
print("All equations as a list: "+str(all_equations))
result = sympy.solve(all_equations, ('x', 'y'))
print("result: "+str(result))
return result
'''
intersection_points = Solve(equation_list, ('x', 'y'))
if len(intersection_points)[0] < 2:
fail("Not enough intersection points for the integral command!")
return 1
intersection_x_values = intersection_points[0]
# make the difference function
#functions_in_y_format = Solve(equation_list, ('y'))
#function1 = functions_in_y_format[0]
functions_in_y_format = []
for eq in equation_list:
functions_in_y_format.append(Solve(eq, ('y')))
intersection_x_values = sorted(intersection_x_values)
check_value = random.uniform(intersection_x_values[0], intersection_x_values[1])
# see which function is larger in that range
if functions_in_y_format[0].subs({'x':check_value}) > functions_in_y_format[1].subs({'x':check_value}):
bigger_function = functions_in_y_format[0]
smaller_fun = functions_in_y_format[1]
else:
bigger_function = functions_in_y_format[1]
smaller_fun = functions_in_y_format[0]
difference_function = parse_expr(bigger_function - smaller_fun)
resulting_area = integrate(difference_function, (x, intersection_x_values[0], intersection_x_values[1]))
print(CYELLOW + "Area: "+str(resulting_area) + ENDC)
return resulting_area
I actually haven’t tested that code yet that it works, so I am going to quickly draw up a command script file which tests it for me:
line a=4 b=-2 c=3
line0.name = myline
area_between_intersections myline y=x**2-10*x+10
quit
and then running this we get an error:
Traceback (most recent call last):
File "geometrylib.py", line 1585, in <module>
command_mainloop(file=filething)
File "geometrylib.py", line 1554, in command_mainloop
handle_functions[index](command_string, global_objects)
File "geometrylib.py", line 1393, in area_between_intersections
expressions = get_object_by_name(selected_object).get_equations()
NameError: name 'selected_object' is not defined
I wanted to showcase just real quick how I debug a bug usually, because i dunno, I think that it is a good idea. I haven’t described my debugging process in this blog post yet until not.
Except that this is a boring bug since that variable should just be the object_name which we declared previously. facepalm . Anyway.
After a couple of type fixes I get this error:
Traceback (most recent call last):
File "geometrylib.py", line 1585, in <module>
command_mainloop(file=filething)
File "geometrylib.py", line 1554, in command_mainloop
handle_functions[index](command_string, global_objects)
File "geometrylib.py", line 1456, in area_between_intersections
if functions_in_y_format[0].subs({'x':check_value}) > functions_in_y_format[1].subs({'x':check_value}):
AttributeError: 'list' object has no attribute 'subs'
Then doing print(“functions_in_y_format == “+str(functions_in_y_format)) before the crash shows this: functions_in_y_format == [[2*x + 3/2], [x**2 - 10*x + 10]] So instead of using only [0] as the index we should use [0][0] instead to get the actual element. This is quite a simple bug, but I just wanted to showcase how I debug stuff. Just slap a debug statement and the see the value and see how the way you are accessing that value goes wrong.
Another bug which I found was that I accidentally typed intersection_x_values = intersection_points[0] instead of intersection_x_values = [intersection_points[0][0], intersection_points[1][0]] After fixing that it works perfectly.
Adding even more features.
Here are a couple of features which I would like to add:
- Add a polygon object or atleast a triangle.
- Way to compute angles and add an angle object. (Basically use stuff like the law of sines to compute them etc etc.)
- 3D-objects.
- Add a line to a point which has a certain angle.
- Default arguments. (if an argument is not given to a function then it assumes that a certain argument has a certain value instead of erroring out.)
The idea for the triangle is to basically just construct it out of three lines by solving the equation ax0+by0+c=0 ax1+by1+c=0 etc and assuming that c is one because reasons.
I implemented a method set_lines_from_points for the triangle object which takes three points and constructs lines from them for the triangle.
A peculiar bug in my system which I came across is this:
Traceback (most recent call last):
File "geometrylib.py", line 1970, in <module>
command_mainloop(file=filething)
File "geometrylib.py", line 1939, in command_mainloop
handle_functions[index](command_string, global_objects)
File "geometrylib.py", line 1138, in point_command
common_object_creation_stuff(args, "point", objects)
File "geometrylib.py", line 1083, in common_object_creation_stuff
arg_dict = dict([thing.split("=")[0], thing.split("=")[1]] for thing in arguments)
File "geometrylib.py", line 1083, in <genexpr>
arg_dict = dict([thing.split("=")[0], thing.split("=")[1]] for thing in arguments)
IndexError: list index out of range
when running python3 geometrylib.py –file thing.txt .
I changed the way that arguments are handled and they no longer work correctly for other commands. This is because the commands do not return the result in a well defined format, but instead if varies from command to command. I should really make the functions return the answers in a specific format instead of just however.
To fix this I added this:
resulting_dict = {'x':result[0][0], 'y':result[0][1]}
print("Resulting dict: "+str(resulting_dict))
oofstring1 = str(result[0][0])
oofstring2 = str(result[0][0])
print("oofstring1: "+str(oofstring1))
print("oofstring2: "+str(oofstring2))
oofstring1 = ''.join(oofstring1.split(" ")) # get rid of spaces
oofstring2 = ''.join(oofstring2.split(" "))
print("oofstring1 after: "+str(oofstring1))
print("oofstring2 after: "+str(oofstring2))
final_dict = {'x':oofstring1, 'y':oofstring2}
print("final_dict: "+str(final_dict))
return final_dict
To the mindistpointobjdot function and now it works well.
To implement the triangle object, we need to make a list of three line equations which each corresponds to the sides of the triangle. Now the thing is that I couldn’t find a way to find all solutions to a set of equations which satisfy atleast one of the equations so I am going to need to modify the code to handle these cases.
In the intersection command I need to do something like this:
def intersection(object1, object2):
# object is assumed to have the get_equation method which returns the equation which describes the object (like a line is a*x+b*y+c=0 )
print("================================================")
print("object1 : " + str(object1))
print("object2 : " + str(object2))
print("object1 : " + str(type(object1)))
print("object2 : " + str(type(object2)))
print("================================================")
equations1 = object1.get_equations()
equations2 = object2.get_equations()
plain_eqs = True
for eq in equations1:
if isinstance(eq, list):
plain_eqs = False
break
if plain_eqs:
for eq in equations2:
if isinstance(eq, list):
plain_eqs = False
break
if plain_eqs: # they are plain equations without any constraints (aka a line and a point for example)
all_equations = equations1 + equations2
print("All equations as a list: "+str(all_equations))
result = sympy.solve(all_equations, ('x', 'y'))
print("result: "+str(result))
else:
result = []
plain_eqs = []
or_eqs1 = []
or_eqs2 = []
for eq in equations1:
if not isinstance(eq, list):
plain_eqs.append(eq)
else:
or_eqs1.append(eq)
for eq in equations2:
if not isinstance(eq, list):
plain_eqs.append(eq)
else:
or_eqs2.append(eq)
if or_eqs1 != [] and or_eqs2 != []:
for or_eq1 in or_eqs1:
for or_eq2 in or_eqs2:
result.append(solve([or_eq1, or_eq2]+plain_eqs), ('x', 'y'))
elif or_eqs1 != [] and or_eqs2 == []:
for or_eq1 in or_eqs1:
result.append(solve([or_eq1]+plain_eqs), ('x', 'y'))
elif or_eqs1 == [] and or_eqs2 != []:
for or_eq2 in or_eqs2:
result.append(solve([or_eq2]+plain_eqs), ('x', 'y'))
else:
# We should not reach this point here.
print("Something went wrong in intersection.")
exit(1)
return result
This piece of code basically checks that if the equation in the equation list returned by get_equations is a list of equations, then get all the solutions which satisfy atleast of one of those equations and all of the other equations. This is used for the triangle object for example, because in the intersection command for example between a line and a triangle we check the intersection between each of the sides of the triangle and the line separately and then append those solutions to the final intersection result list. I actually need to do this for some other places like in distance_min , so instead of copypasting this function everywhere in the code, lets just define a function:
def solve_equation_stuff(object_list, variable):
equations = []
for obj in object_list:
stuff = obj.get_equations()
if isinstance(stuff, list):
# this is for compatibility if the get_equations function returns a list of equations
equations += stuff
else:
equations.append(stuff)
plain_eqs = True
for eq in equations:
if isinstance(eq, list):
plain_eqs = False
break
if plain_eqs: # they are plain equations without any constraints (aka a line and a point for example)
all_equations = equations
print("All equations as a list: "+str(all_equations))
result = sympy.solve(all_equations, ('x', 'y'))
print("result: "+str(result))
else:
result = []
or_eqs = []
plain_eqs = []
for eq in equations:
if not isinstance(eq, list):
plain_eqs.append(eq)
else:
or_eqs.append(eq)
for or_eq1 in or_eqs:
result.append(solve([or_eq1]+plain_eqs), ('x', 'y'))
return result
Writing a testsuite thing:
Now lets put the triangle thing on the backburner for a second, because I honestly need to program a testset thing for this program because otherwise it gets way too messy to deal with stuff.
Now I just quickly hacked this together (the command mainloop function is starting to get quite cluttered I know):
def command_mainloop(file=None, testsuite=None):
print_banner()
line_counter = 0
lines = []
if file:
fh = open(file, "r")
lines = fh.readlines()
fh.close()
for i in range(len(lines)):
lines[i] = lines[i][:-1]
print("Running commands from file "+str(file)+".")
if testsuite:
fh = open(testsuite, "r")
lines = fh.readlines()
fh.close()
for i in range(len(lines)):
lines[i] = lines[i][:-1]
print("Testsuite from file "+str(testsuite)+".")
objects = []
commands = ["line", "intersect", "help", "quit", "objects", "circle", "point", "mindistobjdot", "maxdistobjdot", "mindistpointobjdot", "maxdistpointobjdot", "integrate", "area_between_intersections"]
min_arg_lengths = [0,0,0,0,0,0,0,2,2,2,2,4,2]
max_arg_lengths = [3,2,0,0,0,3,2,2,2,2,2,4,2]
command_result = None
handle_functions = [line_command, intersection_command, help_command, quit_command, objects_command, circle_command, point_command, mindistobjdot, maxdistobjdot, mindistpointobjdot, maxdistpointobjdot, integrate_command, area_between_intersections]
expected_result = None
if testsuite:
expected_result = parse_expected(testsuite)
while True:
if not testsuite:
if line_counter != len(lines):
command_string = lines[line_counter]
line_counter += 1
print("Command string: " + str(command_string))
else:
command_string = str(input(bcolors.OKBLUE + ">>> " + bcolors.ENDC))
#command_string = "line a=1 b=2 c=3"
else:
if line_counter != len(lines):
command_string = lines[line_counter]
line_counter += 1
print("Command string: " + str(command_string))
else:
# check the final output:
print("The output of the last command: "+str(command_result))
print("Expected final result: "+str(expected_result))
if str(command_result) != str(expected_result):
print("Testsuite failed!")
command_start = command_string.split(" ")[0]
if command_start == "quit":
if testsuite:
print("\"quit\" encountered in testsuite. Checking answer:")
break
command_result = None
if command_start not in commands:
if ":=" in command_string: # check variable assignment command
print("poopooshit")
result = variable_assignment_command(command_string, global_objects, max_arg_lengths, min_arg_lengths, commands)
if result:
fail("Invalid command: "+str(command_string))
continue
if command_start != "":
print("thing")
if len(command_string.split(" ")) == 1 and "." not in command_string.split(" ")[0]:
# if the user types just the object name, then print object as string
if command_start in get_names(global_objects):
command_result = print_object(get_object_by_name(command_start))
continue
invalid_command(command_string)
continue
# first assume that the command is an attempt to run a method on an object:
result = check_method_command(command_string, global_objects)
print("result: "+str(result))
if result: # 0 means success, 1 means failure
invalid_command(command_string)
continue
index = commands.index(command_start)
result = check_common_syntax(command_string, max_arg_lengths, min_arg_lengths, commands) # this check is shared by every command to check the arguments
if result:
continue
command_string = unpack_variables_in_command(command_string, user_defined_variables) # this is to unpack arguments like [myvar]
command_result = handle_functions[index](command_string, global_objects)
print("Command result: " + str(command_result))
#global_objects =
print("The output of the last command: "+str(command_result))
print("Expected final result: "+str(expected_result))
if str(command_result) != str(expected_result):
print_col(bcolors.FAIL, "Testsuite " + str(testsuite)+ " failed!")
else:
print_col(bcolors.OKGREEN, "Testsuite " +str(str(testsuite))+ " passed!")
return command_result
and this:
if __name__=="__main__":
'''
if sys.argv[-1] == "--test":
debug_tests()
exit(0)
'''
if "--file" in sys.argv:
filething = sys.argv[sys.argv.index("--file")+1]
else:
filething = None
if "--testsuite" in sys.argv:
testsuite = sys.argv[sys.argv.index("--testsuite")+1]
else:
testsuite = None
test_all = False
if "--test-all" in sys.argv:
test_all = True
if "--get-expected" in sys.argv:
results = []
for test in os.listdir("tests/"):
print("Running test "+str(test))
results.append(command_mainloop(file=filething, testsuite="tests/"+str(test)))
print("Expected values for the tests:")
count = 0
for filething in os.listdir("tests/"):
print("tests/"+filething+" : "+str(results[count]))
count += 1
exit(0)
if not test_all:
command_mainloop(file=filething, testsuite=testsuite)
else:
results = []
for test in os.listdir("tests/"):
print("Running test "+str(test))
_, passing = command_mainloop(file=filething, testsuite="tests/"+str(test))
results.append(passing)
#print summary
count = 0
fail = False
print_col(bcolors.OKBLUE, "=================================================\n\n")
print_col(bcolors.OKBLUE, "Final results: \n")
for thing in os.listdir("tests/"):
if results[count]:
# pass
print_col(bcolors.OKGREEN, "Test: tests/"+str(thing)+" PASSED!")
else:
# fail:
print_col(bcolors.FAIL, "Test: tests/"+str(thing)+" FAILED!")
fail=True
print("\n\n")
if fail:
print_col(bcolors.FAIL, "Some tests failed!\n\n")
else:
print_col(bcolors.OKGREEN, "All tests passed!\n\n")
print_col(bcolors.OKBLUE, "=================================================")
the –get-expected flag gets all of the expected values for the testsuite files and then the –test-all checks all of them. The idea is that before making modifications you update the tests with the –get-expected values (which I should probably also automate, that the program automatically appends the expected values to the testsuite files but oh well) and then after you have done modifications to the program then you later run the test set with –test-all to see that it behaves similarly as to before, because if it doesn’t then you have royally screwed something up.
Trying out the triangle feature:
Now that we have the triangle implemented lets actually try to use it:
First we need to implement a command which lets us create a triangle:
def triangle_command(command:str, objects:list):
args = command.split(" ")
args = args[1:]
common_object_creation_stuff(args, "triangle", objects)
return 0
I am really glad that i programmed that common_object_creation_stuff function so that I don’t have to copy paste code. In fact I don’t even think that the “line_command” and “triangle_command” functions are even necessary, because we could handle that stuff in the mainloop but idk.
Now lets create a quick file which uses this new command and tries to find intersections between the triangle and a line:
triangle x0=0 y0=0 x1=1 y0=0 x2=1 y2=1
line a=0 b=1 c=-0.5
intersect triangle0 line0
quit
and as expected we get an error:
oof
oof22
equations: [[False], [False], [False], Eq(x + y - 0.5, 0)]
or_eq1 : [False]
plain_eqs: []
Traceback (most recent call last):
File "geometrylib.py", line 2203, in <module>
command_mainloop(file=filething, testsuite=testsuite)
File "geometrylib.py", line 2130, in command_mainloop
command_result = handle_functions[index](command_string, global_objects)
File "geometrylib.py", line 1285, in intersection_command
results = intersection(obj1, obj2)
File "geometrylib.py", line 1022, in intersection
results = solve_equation_stuff([object1, object2], ('x','y'))
File "geometrylib.py", line 1005, in solve_equation_stuff
result.append(solve([or_eq1]+plain_eqs), variables)
File "/usr/local/lib/python3.8/dist-packages/sympy-1.9.dev0-py3.8.egg/sympy/solvers/solvers.py", line 856, in solve
symbols = set().union(*[fi.free_symbols for fi in f])
File "/usr/local/lib/python3.8/dist-packages/sympy-1.9.dev0-py3.8.egg/sympy/solvers/solvers.py", line 856, in <listcomp>
symbols = set().union(*[fi.free_symbols for fi in f])
AttributeError: 'list' object has no attribute 'free_symbols'
This is because the parse_expr function also evaluates the equations in addition to simply parsing them so an expression like “x>2” which is a constraint gets simplified to “1>2” if x is one and this of course evaluates to False.
This peculiar bug was solved like this:
final_equation = Eq(parse_expr(equation))
constraint_stuff = parse_expr(constraint_thing)
print("Final equation: "+str(final_equation))
print("Value of x: "+str(parse_expr('x')))
Just simply parsing an expression like “x>2” makes it an equation so no need to do something like Eq(“x>2”) because that won’t work.
Now after that we observe that plain_eqs remains empty for some reason so lets investigate this code:
for eq in equations:
if not isinstance(eq, list):
plain_eqs.append(eq)
else:
or_eqs.append(eq)
for or_eq1 in or_eqs:
print("or_eq1 : "+str(or_eq1))
print("plain_eqs: "+str(plain_eqs))
result.append(solve([or_eq1]+plain_eqs), variables)
This was simply because we indented the code a bit too much it should be like this:
for eq in equations:
print
if not isinstance(eq, list):
plain_eqs.append(eq)
else:
or_eqs.append(eq)
print("Final plain_eqs: "+str(plain_eqs))
for or_eq1 in or_eqs:
print("or_eq1 : "+str(or_eq1))
print("plain_eqs: "+str(plain_eqs))
result.append(solve(or_eq1+plain_eqs), variables)
Now running the code we end up with this:
NotImplementedError:
inequality has more than one symbol of interest
Now, this error is because sympy can not handle inequalities in a certain way. If we try to do something like this:
from sympy import *
x = Symbol('x')
y = Symbol('y')
solve([Eq(x + y - 0.5, 0), Eq(1 - 10.0*y, 0), x <= 1], [x,y])
We get the exact same error. This is complete bullshit because we obviously need this for this thing to work. One workaround which I can see is that we first compute the solution without any restrictions and then afterwards check them.
After a bit of tinkering I got it to work but the thing is that it now ignores the restrictions completely. Anywa, I am going to fix that tomorrow.
Ok so now after a bit of coding I finally came up with this:
def solve_equation_stuff(object_list, variables):
equations = []
for obj in object_list:
stuff = obj.get_equations()
if isinstance(stuff, list):
# this is for compatibility if the get_equations function returns a list of equations
equations += stuff
else:
equations.append(stuff)
plain_eqs = True
for eq in equations:
if isinstance(eq, list):
plain_eqs = False
break
if plain_eqs: # they are plain equations without any constraints (aka a line and a point for example)
all_equations = equations
print("All equations as a list: "+str(all_equations))
result = sympy.solve(all_equations, variables)
print("result: "+str(result))
else:
result = []
or_eqs = []
plain_eqs = []
print("equations: "+str(equations))
for eq in equations:
print
if not isinstance(eq, list):
plain_eqs.append(eq)
else:
or_eqs.append(eq)
print("Final plain_eqs: "+str(plain_eqs))
for or_eq1 in or_eqs:
restriction_thing = []
print("or_eq1 : "+str(or_eq1))
print("plain_eqs: "+str(plain_eqs))
poplist = []
for i in range(len(or_eq1)):
if ">=" in str(or_eq1[i]) or "<=" in str(or_eq1[i]):
poplist.append(i)
restriction_thing.append(or_eq1[i])
'''
# big thanks to https://stackoverflow.com/questions/11303225/how-to-remove-multiple-indexes-from-a-list-at-the-same-time
indexes = [2, 3, 5]
for index in sorted(indexes, reverse=True):
del my_list[index]
'''
for index in sorted(poplist, reverse=True):
del or_eq1[index]
#result.append(solve(or_eq1+plain_eqs, variables))
thing = solve(or_eq1+plain_eqs, variables)
print("Thing stuff: ")
print("restriction_thing: "+str(restriction_thing))
print("thing: "+str(thing))
if isinstance(thing, list):
# handle the list thing:
# this is for when there are multiple solution stuff:
if len(thing) > 1:
# handle multiple solutions aka check them all sequentially
print("poopoo")
#exit(1)
for sol in thing:
if isinstance(sol, dict):
# handle multiple dictionary stuff
thing = sol
for restriction in restriction_thing:
print("current restriction: "+str(restriction))
print("substitution: "+str(thing))
passing = True
oofthing = restriction[0]
for restriction_expr in restriction:
oofthing = (restriction_expr).subs(thing)
if oofthing == False:
passing = False
break
if passing:
result.append(thing)
else:
if len(sol) == 2:
thing = {"x":sol[0], "y":sol[1]}
elif len(sol) == 1:
thing = {"x":sol[0]}
else:
fail("Invalid length for solution thing in solve_equation_stuff:")
print("sol: "+str(sol))
exit(1)
# this is basically for when they are tuples or lists.
# for example in the intersection between a triangle and a circle: [(0.648031893339682, 0.141338648889947), (1.02764378233599, 0.204607297055999)]
for restriction in restriction_thing:
print("current restriction: "+str(restriction))
print("substitution: "+str(thing))
passing = True
oofthing = restriction[0]
for restriction_expr in restriction:
oofthing = (restriction_expr).subs(thing)
if oofthing == False:
passing = False
break
if passing:
result.append(thing)
else:
thing = thing[0]
for restriction in restriction_thing:
print("current restriction: "+str(restriction))
print("substitution: "+str(thing))
passing = True
oofthing = restriction[0]
for restriction_expr in restriction:
oofthing = (oofthing).subs(thing)
if oofthing == False:
passing = False
break
if passing:
result.append(thing)
else:
for restriction in restriction_thing:
print("current restriction: "+str(restriction))
print("substitution: "+str(thing))
passing = True
oofthing = restriction[0]
for restriction_expr in restriction:
oofthing = (oofthing).subs(thing)
if oofthing == False:
passing = False
break
if passing:
result.append(thing)
#if (restriction).subs(thing):
# print("passed this: "+str(restriction)+" "+str(thing))
# result.append(thing)
return result
Which is way more convoluted than it has to be, but it does the job. Now finally I can do this:
triangle x0=0.4 y0=0.1 x1=1 y1=0.2 x2=1 y2=1
line a=0.1 b=1 c=-0.5
intersect triangle0 line0
quit
and it produces the right results:
[{x: 0.625000000000000, y: 0.437500000000000}, {x: 1.00000000000000, y: 0.400000000000000}]
Now another thing which I would like to implement is a way to get an angle between two line objects, because that makes it a lot easier to calculate for example the angles inside a triangle. The angle between a line and the x axis is arctan(-a/b) therefore the line between two lines is:
abs(abs(arctan(-a1/b1))-abs(arctan(-a2/b2)))
When the lines are a1x+b1y+c=0 and a2xx+b2y+c=0
For example in the next picture we have x+2y+3=0 and 4x+5*y+6=0
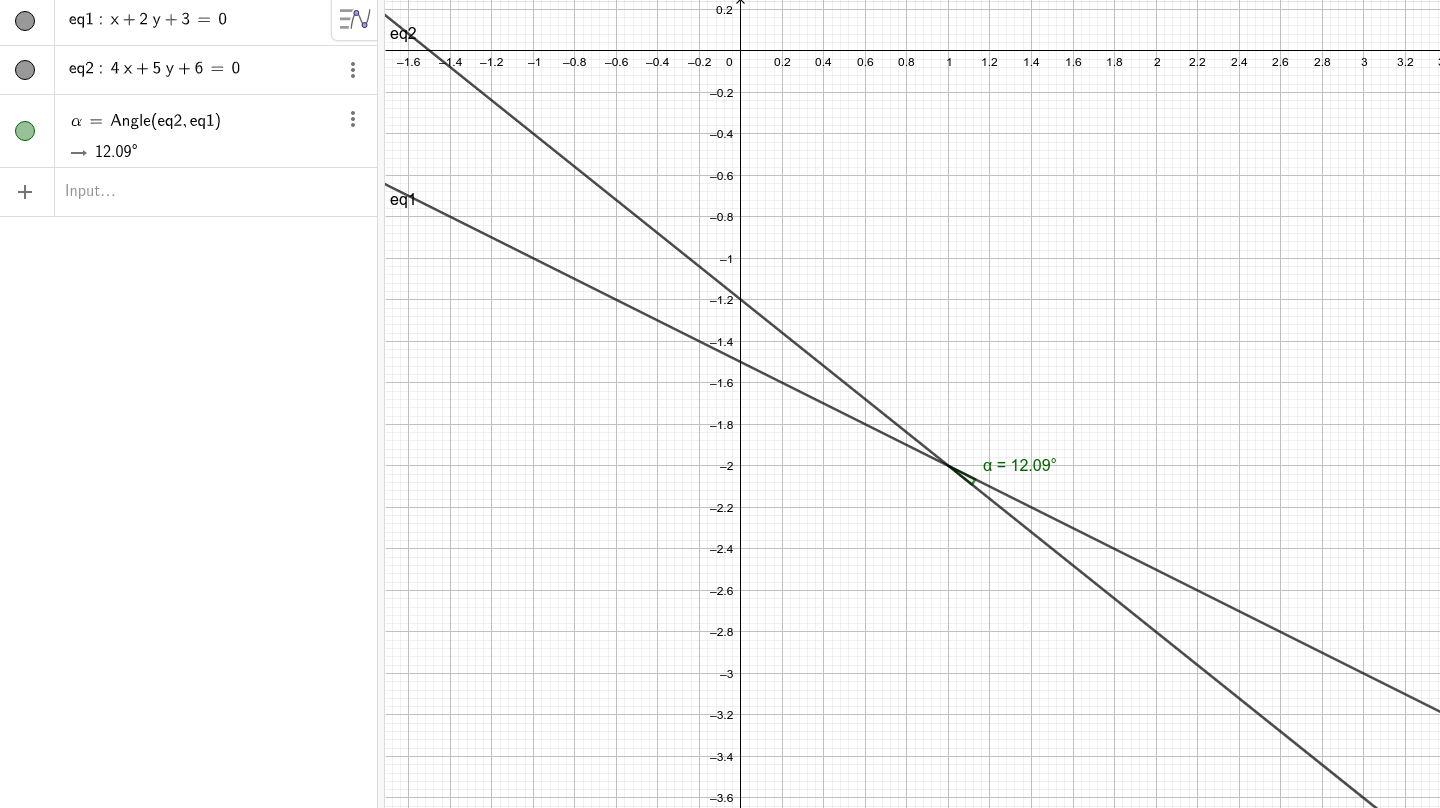
and the angle is around 12.09 degrees .
Lets use the formula and check our work:
abs(abs(arctan(-a1/b1))-abs(arctan(-a2/b2)))
in xcas:
a1:=1
b1:=2
a2:=4
b2:=5
abs(arctan(-a1/b1)-arctan(-a2/b2))
results is:
12.094757077
so our formula works. Lets put it into the program:
def angle_between_lines(line1, line2):
result = simplify(parse_expr("Abs(atan(-{}/{})-atan(-{}/{}))".format(str(line1.a), str(line1.b), str(line2.a), str(line2.b))))
# it is in radians so convert to degrees.
result *=360
result /= 2
result /= 3.14159265358979323846 # pi
return result
and the command thing:
def angle_between_lines_command(command:str, objects:list):
# returns the angle between two lines
args = command.split(" ")
args = args[1:]
first_line = get_object_by_name(args[0])
second_line = get_object_by_name(args[1])
final_result = angle_between_lines(first_line, second_line)
print_col(bcolors.OKBLUE, "Angle between lines: "+str(final_result)+" == " + str((final_result).evalf()))
return (final_result).evalf()
One thing which actually stood out to me was that the tests passed on the first try so I was a bit sceptical of that. Looking through the code the code was originally this:
for thing in os.listdir("tests/"):
if results[count]:
# pass
print_col(bcolors.OKGREEN, "Test: tests/"+str(thing)+" PASSED!")
else:
# fail:
print_col(bcolors.FAIL, "Test: tests/"+str(thing)+" FAILED!")
fail=True
print("\n\n")
if fail:
print_col(bcolors.FAIL, "Some tests failed!\n\n")
else:
print_col(bcolors.OKGREEN, "All tests passed!\n\n")
print_col(bcolors.OKBLUE, "=================================================")
We do not increment the “count” variable so if the first test passes then this code incorrectly reports that every test passed so we need to increment the count variable like so:
for thing in os.listdir("tests/"):
if results[count]:
# pass
print_col(bcolors.OKGREEN, "Test: tests/"+str(thing)+" PASSED!")
else:
# fail:
print_col(bcolors.FAIL, "Test: tests/"+str(thing)+" FAILED!")
fail=True
count += 1
print("\n\n")
if fail:
print_col(bcolors.FAIL, "Some tests failed!\n\n")
else:
print_col(bcolors.OKGREEN, "All tests passed!\n\n")
print_col(bcolors.OKBLUE, "=================================================")
Also another issue which I faced was that the environment had to be reset in between each testsuite file because otherwise the definition of variables in the last testsuite screws stuff up in the next testsuite.
Implementing tangents
Another feature to add is adding tangents to this program. We get a tangentline on a point on an object. We also could probably make a tangent thing for many object to get all tangentlines which are tangent to two or more objects (if there are any).
To do this just use the line passing through a point formula and the derivative of the function at that point for the derivative of the tangent:
def get_tangents(objects:list):
# get the tangentlines which are shared by all the objects (if there exists any)
if len(objects) == 1:
# just get the tangent line stuff at x=x0 and return it
# triangles are not supported because reasons.
# the point is (x0,f(x0)) and the derivative aka k is derivative(f(x),x)|x=x0
obj = objects[0]
equation_list = obj.get_equations()
# first solve y from the equation
#y_eqs = []
tangent_lines = []
for eq in equation_list:
y_eqs = solve(eq, 'y')
for y_eq in y_eqs:
#k = simplify(derivative(y_eq, x))
x0 = Symbol('x0')
print("y_eq: "+str(y_eq))
print("equation_list: "+str(equation_list))
tangent = get_tangent_from_point_and_derivative(x0,y_eq.subs({"x":x0}))
tangent = tangent.subs({"xnew":x0})
tangent_lines.append(tangent)
return tangent_lines
and:
def get_tangent_from_point_and_derivative(x0thing,fx0):
xnew = Symbol('xnew')
x0 = Symbol('x0')
x = Symbol('x')
k = simplify(Derivative(fx0,x0thing)).subs({str(x0thing):xnew})
print("k : "+str(k))
# y - y0 = k*(x - x0)
print("x0 : "+str(x0))
print("fx0 : "+str(fx0))
derivative_line = simplify(k*(x - x0thing.subs({x0thing:xnew})) + fx0.subs({str(x0thing):xnew}))
print("derivative_line: "+str(derivative_line))
return derivative_line
and here is a testuite which I made:
circle xc=0 yc=0 r=1
circle0.name = mycircle
tangents mycircle
quit
#[(x*x0 - 1)/sqrt(1 - x0**2), (-x*x0 + 1)/sqrt(1 - x0**2)]
And it passes all of the tests. Nice! Now we can get a tangent of one object. In addition to getting a tangent of one object I would like to also get a shared tangent between two objects aka tangent lines which are tangent to two objects at the same time but I will save that for later.
Implementing common tangents:
To implement a way to solve for tangent lines which are shared upon many objects is to find a line which are in both groups of all possible tangent lines for each object. To do this we need to implement a function which checks if a line is the same line as another line.
Because an object may have multiple equations describing it, we need to run through every one of them for every object, and since there may be any arbitrary amount of objects, we need to basically do this bullshit for every one of them.
Now running this script:
circle xc=0 yc=0 r=1
circle0.name = circleone
circle xc=2 yc=0 r=1
circle0.name = circletwo
tangents circleone circletwo
quit
Results in this output:
Welcome to geometrylib 1.0 !
Type "help" for help menu.
Running commands from file ./tests/check_common_tangent.txt.
Command string:
Command string: circle xc=0 yc=0 r=1
fewfeewfewfewf
arguments: ['xc=0', 'yc=0', 'r=1']
object_name: circle
{'xc': '0', 'yc': '0', 'r': '1'}
*arguments_thing : {'xc': '0', 'yc': '0', 'r': '1'}
bullshit: {'xc': '0', 'yc': '0', 'r': '1'}
bullshit: {'xc': '0', 'yc': '0', 'r': '1'}
the_object.name == circle0
setting parameter xc to this: xc0
the_object.name == circle0
setting parameter yc to this: yc0
the_object.name == circle0
setting parameter r to this: r0
the_object.name == circle0
setting parameter x to this: x0
the_object.name == circle0
setting parameter y to this: y0
Names of global objects at the end of common_arg_stuff: []
global_objects at the start: []
objects after creation of new_object : []
gregregregrr
global_objects at the start: ['circle0']
objects after appending new_object: ['circle0']
global_objects after appending new_object: ['circle0']
Created new object.
Command result: 0
Command string: circle0.name = circleone
thing
==================================================================================
Setting property : name
On object: circle0
selected_property: name
value: circleone
self.yc : 0
result: None
Command string: circle xc=2 yc=0 r=1
fewfeewfewfewf
arguments: ['xc=2', 'yc=0', 'r=1']
object_name: circle
{'xc': '2', 'yc': '0', 'r': '1'}
*arguments_thing : {'xc': '2', 'yc': '0', 'r': '1'}
bullshit: {'xc': '2', 'yc': '0', 'r': '1'}
bullshit: {'xc': '2', 'yc': '0', 'r': '1'}
the_object.name == circle0
setting parameter xc to this: xc0
the_object.name == circle0
setting parameter yc to this: yc0
the_object.name == circle0
setting parameter r to this: r0
the_object.name == circle0
setting parameter x to this: x0
the_object.name == circle0
setting parameter y to this: y0
Names of global objects at the end of common_arg_stuff: ['circleone']
global_objects at the start: ['circleone']
objects after creation of new_object : ['circleone']
gregregregrr
global_objects at the start: ['circleone', 'circle0']
objects after appending new_object: ['circleone', 'circle0']
global_objects after appending new_object: ['circleone', 'circle0']
Created new object.
Command result: 0
Command string: circle0.name = circletwo
thing
==================================================================================
Setting property : name
On object: circle0
selected_property: name
value: circletwo
self.yc : 0
result: None
Command string:
Command string: tangents circleone circletwo
fewfeewfewfewf
name_str: circleone
['circleone', 'circletwo']
---------------------------
circleone
circletwo
---------------------------
name_str: circletwo
['circleone', 'circletwo']
---------------------------
circleone
circletwo
---------------------------
obj.name == circleone
Circle equation bullshit:
((x)-(0))**2+((y)-(0))**2=(1)**2
oof
oof22
y_eq: -sqrt(1 - x**2)
equation_list: [Eq(x**2 + y**2, 1)]
k : xnew/sqrt(1 - xnew**2)
x0 : x0
fx0 : -sqrt(1 - x0**2)
derivative_line: (x*xnew - 1)/sqrt(1 - xnew**2)
y_eq: sqrt(1 - x**2)
equation_list: [Eq(x**2 + y**2, 1)]
k : -xnew/sqrt(1 - xnew**2)
x0 : x0
fx0 : sqrt(1 - x0**2)
derivative_line: (-x*xnew + 1)/sqrt(1 - xnew**2)
Circle equation bullshit:
((x)-(2))**2+((y)-(0))**2=(1)**2
oof
oof22
y_eq: -sqrt(-(x - 3)*(x - 1))
equation_list: [Eq(y**2 + (x - 2)**2, 1)]
k : sqrt(-(xnew - 3)*(xnew - 1))*(2 - xnew)/((xnew - 3)*(xnew - 1))
x0 : x0
fx0 : -sqrt(-(x1 - 3)*(x1 - 1))
derivative_line: (x*xnew - 2*x - 2*xnew + 3)/sqrt(-xnew**2 + 4*xnew - 3)
y_eq: sqrt(-(x - 3)*(x - 1))
equation_list: [Eq(y**2 + (x - 2)**2, 1)]
k : -sqrt(-(xnew - 3)*(xnew - 1))*(2 - xnew)/((xnew - 3)*(xnew - 1))
x0 : x0
fx0 : sqrt(-(x1 - 3)*(x1 - 1))
derivative_line: sqrt(-(xnew - 3)*(xnew - 1))*((x - xnew)*(xnew - 2) + (xnew - 3)*(xnew - 1))/((xnew - 3)*(xnew - 1))
Running run_through_list:
thing1: (x*x0 - 1)/sqrt(1 - x0**2)
thing2: (x*x1 - 2*x - 2*x1 + 3)/sqrt(-x1**2 + 4*x1 - 3)
Solution stuff: [(sqrt(1 - x0**2)/sqrt(-x1**2 + 4*x1 - 3), x0, y0, x1, y1)]
thing1: (x*x0 - 1)/sqrt(1 - x0**2)
thing2: sqrt(-(x1 - 3)*(x1 - 1))*((x - x1)*(x1 - 2) + (x1 - 3)*(x1 - 1))/((x1 - 3)*(x1 - 1))
Solution stuff: [(-sqrt(1 - x0**2)/sqrt(-x1**2 + 4*x1 - 3), x0, y0, x1, y1)]
thing1: (-x*x0 + 1)/sqrt(1 - x0**2)
thing2: (x*x1 - 2*x - 2*x1 + 3)/sqrt(-x1**2 + 4*x1 - 3)
Solution stuff: [(-sqrt(1 - x0**2)/sqrt(-x1**2 + 4*x1 - 3), x0, y0, x1, y1)]
thing1: (-x*x0 + 1)/sqrt(1 - x0**2)
thing2: sqrt(-(x1 - 3)*(x1 - 1))*((x - x1)*(x1 - 2) + (x1 - 3)*(x1 - 1))/((x1 - 3)*(x1 - 1))
Solution stuff: [(sqrt(1 - x0**2)/sqrt(-x1**2 + 4*x1 - 3), x0, y0, x1, y1)]
Final solutions: [(sqrt(1 - x0**2)/sqrt(-x1**2 + 4*x1 - 3), x0, y0, x1, y1)]
Command result: None
Command string: quit
fewfeewfewfewf
Thank you for using geometrylib! See you again soon!
Obviously this is wrong.
Lets draw a picture of the situation in a graphing calculator:
t = (sqrt(1 - x02)/sqrt(-x12 + 4*x1 - 3)
(xb - 2x - 2b + 3)/sqrt(-b^2 + 4b - 3)
thing1: (x*x0 - 1)/sqrt(1 - x0**2)
thing2: (x*x1 - 2*x - 2*x1 + 3)/sqrt(-x1**2 + 4*x1 - 3)
Solution stuff: [(sqrt(1 - x0**2)/sqrt(-x1**2 + 4*x1 - 3), x0, y0, x1, y1)]
i am going to mark x0 as a, x1 as b, y0 as c and y1 as d
t = sqrt(1 - (x0^2))/sqrt(-(x1^2) + 4*x1 - 3)
t = sqrt(1 - (a^2))/sqrt(-(b^2) + 4*b - 3)
f(x) = (xb - 2x - 2b + 3)/sqrt(-(b^2) + 4b - 3)*t
l(x) = (x*a - 1)/sqrt(1 - a^2)
I think that this is because the approach I am taking for solving the tangents is wrong, see I am checking if the lines are the same, but instead I want to check that their derivatives are the same and they pass through the same points.
(-sqrt(x1*2 - 4x1 + 4), y0, x1, y1), (sqrt(x1*2 - 4x1 + 4), y0, x1, y1)
-sqrt(x1*2 - 4x1 + 4), y0, x1, y1), (sqrt(x1*2 - 4x1 + 4)
Now, there is some peculiar behaviour:
>>> simplify(Derivative(-sqrt(1 - x0**2), x0))
x0/sqrt(1 - x0**2)
>>> solve(Eq(Derivative(-sqrt(1 - x0**2), x0), Derivative(-sqrt(-(x1 - 3)*(x1 - 1)), x1)))
KeyboardInterrupt
>>> simplify(Derivative(-sqrt(-(x1 - 3)*(x1 - 1)), x1)))
File "<stdin>", line 1
simplify(Derivative(-sqrt(-(x1 - 3)*(x1 - 1)), x1)))
^
SyntaxError: unmatched ')'
>>> simplify(Derivative(-sqrt(-(x1 - 3)*(x1 - 1)), x1))
sqrt(-(x1 - 3)*(x1 - 1))*(2 - x1)/((x1 - 3)*(x1 - 1))
>>> (sqrt(-(x1 - 3)*(x1 - 1))*(2 - x1)/((x1 - 3)*(x1 - 1))).subs({x1:0.5})
1.34164078649987*I
>>> (sqrt(-(x1 - 3)*(x1 - 1))*(2 - x1)/((x1 - 3)*(x1 - 1))).subs({x1:2.5})
0.577350269189626
>>> (x0/sqrt(1 - x0**2)).subs({x0:0.5})
0.577350269189626
>>> solve((sqrt(-(x1 - 3)*(x1 - 1))*(2 - x1)/((x1 - 3)*(x1 - 1))))
KeyboardInterrupt
>>> solve(Eq((sqrt(-(x1 - 3)*(x1 - 1))*(2 - x1)/((x1 - 3)*(x1 - 1))), (x0/sqrt(1 - x0**2))), (x1,x0))
[(x0 + 2, x0)]
>>> solve(Eq(Derivative(-sqrt(1 - x0**2), x0), Derivative(-sqrt(-(x1 - 3)*(x1 - 1)), x1)))
[]
>>> solve(Eq(Derivative(-sqrt(1 - x0**2), x0), Derivative(-sqrt(-(x1 - 3)*(x1 - 1)))))
[]
>>> solve(Eq(Derivative(-sqrt(1 - x0**2), x0), Derivative(-sqrt(-(x1 - 3)*(x1 - 1)))), x0)
[]
>>> solve(Eq(Derivative(-sqrt(1 - x0**2), x0), Derivative(-sqrt(-(x1 - 3)*(x1 - 1)))), (x1,x0))
[]
>>> solve(Eq(Derivative(-sqrt(1 - x0**2), x0), Derivative(-sqrt(-(x1 - 3)*(x1 - 1)))))
[]
>>> solve(Eq(Derivative(-sqrt(1 - x0**2, x0)), Derivative(-sqrt(-(x1 - 3)*(x1 - 1)), x1)))
[]
>>> solve(Eq(Derivative(-sqrt(1 - x0**2, x0)), Derivative(-sqrt(-(x1 - 3)*(x1 - 1)), x1)), x0)
[]
>>> solve(Eq(Derivative(-sqrt(1 - x0**2, x0)), Derivative(-sqrt(-(x1 - 3)*(x1 - 1)), x1)))
[]
>>> solve(Eq(Derivative(-sqrt(1 - x0**2), x0), Derivative(-sqrt(-(x1 - 3)*(x1 - 1)), x1)))
[]
>>> solve(Eq(Derivative(-sqrt(1 - x0**2), x0), Derivative(-sqrt(-(x1 - 3)*(x1 - 1)), x1)), x0)
[]
>>> solve(Eq(Derivative(-sqrt(1 - x0**2), x0), Derivative(-sqrt(-(x1 - 3)*(x1 - 1)), x1)))
[]
>>> simplify(Derivative(-sqrt(1 - x0**2), x0))
x0/sqrt(1 - x0**2)
>>> simplify(Derivative(-sqrt(-(x1 - 3)*(x1 - 1)), x1))
sqrt(-(x1 - 3)*(x1 - 1))*(2 - x1)/((x1 - 3)*(x1 - 1))
>>> Eq(Derivative(-sqrt(1 - x0**2), x0), Derivative(-sqrt(-(x1 - 3)*(x1 - 1)), x1))
Eq(Derivative(-sqrt(1 - x0**2), x0), Derivative(-sqrt((3 - x1)*(x1 - 1)), x1))
>>> simplify(Eq(Derivative(-sqrt(1 - x0**2), x0), Derivative(-sqrt(-(x1 - 3)*(x1 - 1)), x1)))
Eq(x0/sqrt(1 - x0**2), sqrt(-(x1 - 3)*(x1 - 1))*(2 - x1)/((x1 - 3)*(x1 - 1)))
>>> solve(Eq(x0/sqrt(1 - x0**2), sqrt(-(x1 - 3)*(x1 - 1))*(2 - x1)/((x1 - 3)*(x1 - 1))),x0)
[x1 - 2]
>>> solve(Eq(x0/sqrt(1 - x0**2), sqrt(-(x1 - 3)*(x1 - 1))*(2 - x1)/((x1 - 3)*(x1 - 1))),(x0,x1))
[(x1 - 2, x1)]
>>> solve(Eq(x0/sqrt(1 - x0**2), sqrt(-(x1 - 3)*(x1 - 1))*(2 - x1)/((x1 - 3)*(x1 - 1))),x0,x1)
[(x1 - 2, x1)]
>>>
Now, I came accross a very peculiar bug. This time the bug I think is actually in the sympy package instead of my own code. I filed this issue to the sympy github page: https://github.com/sympy/sympy/issues/25057 . Lets hope that the devs fix it soon. In the mean time we can just use the simplify for our purposes.
After doing that fix now we get some very strange behaviour. Our tangent in the thing has the correct intersection with the circle, but the derivative is the opposite sign of what it should be.
Ok I found the bug. Originally these lines:
thing_y_1 = solve(thing_y_1, 'y')[counter1]
thing_y_2 = solve(thing_y_2, 'y')[counter2]
where this:
thing_y_1 = solve(thing_y_1, 'y')[0]
thing_y_2 = solve(thing_y_2, 'y')[0]
because I made the assumption that every object had only one equation associated with them.
After the tangents have been determined for two objects, we can then make a very obvious optimization that we can just check that the lines are tangent to the other objects. We do not need to solve for the lines, because the tangents which are tangent between two objects also have to be tangent to those other objects in order for the tangent to be shared by all of them (by definition) . This may give us some problems in the future when we try to implement this stuff in 3d but I think that this is fine for now (that is a problem for future me).
3.12.2023
Ok so it has been a while and I decided to make this tool a bit better. It has actually been around nine months. Time flies. (See the commit history here: https://github.com/personnumber3377/Geometrylib)
I was scrolling youtube and I found this video: https://www.youtube.com/watch?v=qOOnBTaHG_Q . I began to wonder if my tool could accomplish this task. I am going to first clean up the project on github a bit and I am going to remove some unnecessary files and stuff.
Done.
Now it is time to see if I can solve it. First we want to convert the problem into geometric expressions my program can understand.
There are two circles. I am going to call the radius r instead of the scalar value of five, because I like generality. Who doesn’t?
I have to actually remind myself how this tool (which I wrote myself) works.
Does this work?
circle xc=0 yc=0 r=r0
Yes, it works!
Ok, soooo… the other circle should be: circle xc=2*r0 yc=0 r=r0 ? Yeah, that seems to work.
Let’s simplify the problem a bit. We need to find out a point on the circle, such that the distance from the horizontal bottom line is half the distance to the vertical line which is tangent to the circle. The coordinates where the horizontal and vertical point cross each other is r,-r and the slope of the line which represents the distances is -2, so therefore we should add a line which goes through the point (r,-r) and has a slope of -2.
sooo like this???
point
point0.name = firstlinepoint
point
point0.name = secondlinepoint
firstlinepoint.set_point_to_values r0-1 r0+2
secondlinepoint.set_point_to_values r0 r0
line
line0.name = helperline
helperline.set_values_two_points firstlinepoint secondlinepoint
circle xc=0 yc=0 r=r0
intersect circle helperline
Uh oh…
arguments_for_method.append(float(arguments[i]))
^^^^^^^^^^^^^^^^^^^
ValueError: could not convert string to float: 'r0-1'
I programmed this tool in such a way that the functions always expect float inputs, so I should better make a change, such that expressions as inputs are allowed. There is even this comment: # assumed to be a constant: on the next before that line! I was quite dumb nine months ago.
Ok, now I get this:
Command result: [(-sqrt(5*r0**2 - 16)/5 - 8/5, 2*sqrt(5*r0**2 - 16)/5 - 4/5), (sqrt(5*r0**2 - 16)/5 - 8/5, -2*sqrt(5*r0**2 - 16)/5 - 4/5)]
which is this:
(-3.6880613017821102, 3.3761226035642204)
I added a debug statement which prints helperline.
Here is the output stuff:
Welcome to geometrylib 1.0 !
Type "help" for help menu.
Running commands from file circle_thing.txt.
Command string: point
fewfeewfewfewf
arguments: []
object_name: point
{}
*arguments_thing : {}
bullshit: {}
bullshit: {}
the_object.name == point0
setting parameter x to this: x0
the_object.name == point0
setting parameter y to this: y0
Names of global objects at the end of common_arg_stuff: []
global_objects at the start: []
objects after creation of new_object : []
gregregregrr
global_objects at the start: ['point0']
objects after appending new_object: ['point0']
global_objects after appending new_object: ['point0']
Command result: 0
Command string: point0.name = firstlinepoint
thing
==================================================================================
Setting property : name
On object: point0
selected_property: name
value: firstlinepoint
result: None
Command string: point
fewfeewfewfewf
arguments: []
object_name: point
{}
*arguments_thing : {}
bullshit: {}
bullshit: {}
the_object.name == point0
setting parameter x to this: x0
the_object.name == point0
setting parameter y to this: y0
Names of global objects at the end of common_arg_stuff: ['firstlinepoint']
global_objects at the start: ['firstlinepoint']
objects after creation of new_object : ['firstlinepoint']
gregregregrr
global_objects at the start: ['firstlinepoint', 'point0']
objects after appending new_object: ['firstlinepoint', 'point0']
global_objects after appending new_object: ['firstlinepoint', 'point0']
Command result: 0
Command string: point0.name = secondlinepoint
thing
==================================================================================
Setting property : name
On object: point0
selected_property: name
value: secondlinepoint
result: None
Command string: firstlinepoint.set_point_to_values r0-1 r0+2
thing
bullshitrgregreg
command: firstlinepoint.set_point_to_values r0-1 r0+2
self.method_arg_types : [['float', 'float'], []]
self.method_arg_types : [['float', 'float'], []]
SHITSHITSHIT
self.x == r0 - 1
self.y == r0 + 2
x_in: r0 - 1
y_in: r0 + 2
result: 0
Command string: secondlinepoint.set_point_to_values r0 r0
thing
bullshitrgregreg
command: secondlinepoint.set_point_to_values r0 r0
self.method_arg_types : [['float', 'float'], []]
self.method_arg_types : [['float', 'float'], []]
SHITSHITSHIT
self.x == r0
self.y == r0
x_in: r0
y_in: r0
result: 0
Command string: line
fewfeewfewfewf
objects at the start: ['firstlinepoint', 'secondlinepoint']
arguments: []
object_name: line
{}
*arguments_thing : {}
bullshit: {}
bullshit: {}
the_object.name == line0
setting parameter a to this: a0
the_object.name == line0
setting parameter b to this: b0
the_object.name == line0
setting parameter c to this: c0
the_object.name == line0
setting parameter x to this: x0
the_object.name == line0
setting parameter y to this: y0
Names of global objects at the end of common_arg_stuff: ['firstlinepoint', 'secondlinepoint']
global_objects at the start: ['firstlinepoint', 'secondlinepoint']
objects after creation of new_object : ['firstlinepoint', 'secondlinepoint']
gregregregrr
global_objects at the start: ['firstlinepoint', 'secondlinepoint', 'line0']
objects after appending new_object: ['firstlinepoint', 'secondlinepoint', 'line0']
global_objects after appending new_object: ['firstlinepoint', 'secondlinepoint', 'line0']
objects at the end: ['firstlinepoint', 'secondlinepoint', 'line0']
[92mCreated new object.[0m
Command result: 0
Command string: line0.name = helperline
thing
==================================================================================
Setting property : name
On object: line0
selected_property: name
value: helperline
result: None
Command string: helperline.set_values_two_points firstlinepoint secondlinepoint
thing
bullshitrgregreg
command: helperline.set_values_two_points firstlinepoint secondlinepoint
self.method_arg_types : [['point', 'point'], ['point', 'point'], [], []]
name_str: firstlinepoint
['firstlinepoint', 'secondlinepoint', 'helperline']
---------------------------
firstlinepoint
secondlinepoint
helperline
---------------------------
self.method_arg_types : [['point', 'point'], ['point', 'point'], [], []]
name_str: secondlinepoint
['firstlinepoint', 'secondlinepoint', 'helperline']
---------------------------
firstlinepoint
secondlinepoint
helperline
---------------------------
obj.name == firstlinepoint
==========================================
point1.x : r0 - 1 point1.y: r0 + 2
point2.x : r0 point2.y: r0
==========================================
-1*point1.x+point2.x == 1
-1*point1.x == 1 - r0
type(point1.x) == <class 'sympy.core.add.Add'>
xv: 1
yv: -2
0000000
yv: -2
x0: r0 - 1
xv: 1
y0: r0 + 2
string_oof_1 : -(-2/(r0 - 1*-2-1*r0 + 2))
string_oof_2 == 1/(r0 - 1*-2-1*r0 + 2)
self.a ==1/2
self.b ==1/4
result: None
Command string: helperline
thing
name_str: helperline
['firstlinepoint', 'secondlinepoint', 'helperline']
---------------------------
firstlinepoint
secondlinepoint
helperline
---------------------------
obj.name == firstlinepoint
obj.name == secondlinepoint
=======================
Type: line
a = 1/2
b = 1/4
c = 1
name = helperline
=======================
Command string: circle xc=0 yc=0 r=r0
fewfeewfewfewf
arguments: ['xc=0', 'yc=0', 'r=r0']
object_name: circle
{'xc': '0', 'yc': '0', 'r': 'r0'}
*arguments_thing : {'xc': '0', 'yc': '0', 'r': 'r0'}
bullshit: {'xc': '0', 'yc': '0', 'r': 'r0'}
bullshit: {'xc': '0', 'yc': '0', 'r': 'r0'}
the_object.name == circle0
setting parameter xc to this: xc0
the_object.name == circle0
setting parameter yc to this: yc0
the_object.name == circle0
setting parameter r to this: r0
the_object.name == circle0
setting parameter x to this: x0
the_object.name == circle0
setting parameter y to this: y0
Names of global objects at the end of common_arg_stuff: ['firstlinepoint', 'secondlinepoint', 'helperline']
global_objects at the start: ['firstlinepoint', 'secondlinepoint', 'helperline']
objects after creation of new_object : ['firstlinepoint', 'secondlinepoint', 'helperline']
gregregregrr
global_objects at the start: ['firstlinepoint', 'secondlinepoint', 'helperline', 'circle0']
objects after appending new_object: ['firstlinepoint', 'secondlinepoint', 'helperline', 'circle0']
global_objects after appending new_object: ['firstlinepoint', 'secondlinepoint', 'helperline', 'circle0']
[92mCreated new object.[0m
Command result: 0
Command string: intersect circle0 helperline
fewfeewfewfewf
Args : ['intersect', 'circle0', 'helperline']
obj_name1 : circle0
obj_name2 : helperline
name_str: circle0
['firstlinepoint', 'secondlinepoint', 'helperline', 'circle0']
---------------------------
firstlinepoint
secondlinepoint
helperline
circle0
---------------------------
obj.name == firstlinepoint
obj.name == secondlinepoint
obj.name == helperline
name_str: helperline
['firstlinepoint', 'secondlinepoint', 'helperline', 'circle0']
---------------------------
firstlinepoint
secondlinepoint
helperline
circle0
---------------------------
obj.name == firstlinepoint
obj.name == secondlinepoint
poopooo
obj1: =======================
Type: circle
x0 = 0
y0 = 0
r = r0
name = circle0
=======================
obj2: =======================
Type: line
a = 1/2
b = 1/4
c = 1
name = helperline
=======================
================================================
object1 : =======================
Type: circle
x0 = 0
y0 = 0
r = r0
name = circle0
=======================
object2 : =======================
Type: line
a = 1/2
b = 1/4
c = 1
name = helperline
=======================
object1 : <class '__main__.circle'>
object2 : <class '__main__.line'>
================================================
Circle equation bullshit:
((x)-(0))**2+((y)-(0))**2=(r0)**2
oof
oof22
oof
oof22
All equations as a list: [Eq(x**2 + y**2, r0**2), Eq(x/2 + y/4 + 1, 0)]
result: [(-sqrt(5*r0**2 - 16)/5 - 8/5, 2*sqrt(5*r0**2 - 16)/5 - 4/5), (sqrt(5*r0**2 - 16)/5 - 8/5, -2*sqrt(5*r0**2 - 16)/5 - 4/5)]
[33mObjects intersect atleast at one point.[0m
[33mIntersections are at points: [(-sqrt(5*r0**2 - 16)/5 - 8/5, 2*sqrt(5*r0**2 - 16)/5 - 4/5), (sqrt(5*r0**2 - 16)/5 - 8/5, -2*sqrt(5*r0**2 - 16)/5 - 4/5)][0m
Command result: [(-sqrt(5*r0**2 - 16)/5 - 8/5, 2*sqrt(5*r0**2 - 16)/5 - 4/5), (sqrt(5*r0**2 - 16)/5 - 8/5, -2*sqrt(5*r0**2 - 16)/5 - 4/5)]
[94m>>> [0mfewfeewfewfewf
[92mThank you for using geometrylib! See you again soon![0m
and here is the line:
obj2: =======================
Type: line
a = 1/2
b = 1/4
c = 1
name = helperline
=======================
ax + bx + c = 0
actually I had r0+2 when -r0+2 is actually correct.
ok so here is the working prompt:
point
point0.name = firstlinepoint
point
point0.name = secondlinepoint
firstlinepoint.set_point_to_values r0-1 -r0+2
secondlinepoint.set_point_to_values r0 -r0
line
line0.name = helperline
helperline.set_values_two_points firstlinepoint secondlinepoint
helperline
circle xc=0 yc=0 r=r0
intersect circle0 helperline
after that, it is trivial to get the area.
and actually I had to change the {}/({}*{}-{}*{}) to ({})/(({})*({})-({})*({})) in set_values_two_points.
Ok, so this tool is a bit clunky. There are a couple of things to add, for example I could add a way to define a line with a slope and a point, also I could add a way to just parse raw expressions on the command line. (Which aren’t functions or geometry things.)